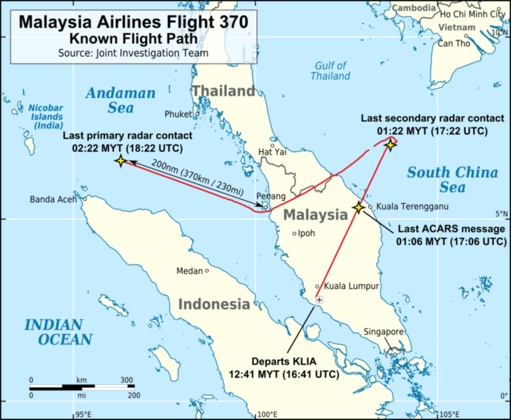We all remember Malaysia Airlines flight 370, that mysteriously disappeared somewhere in the Indian ocean, on March 8, 2014. The flight had left Kuala Lumpur and was bound to Beijing. Normally, it should fly in the north-east direction, towards the Chinese capital.
However, less than an hour after takeoff, it turned westward, for no apparent reason, and eventually vanished from the radar screens.
If some kind of an alarm had been triggered at the air traffic control when the plane made that inexplicable turn, perhaps we would have a better idea of what happened afterwards.
In general, commercial planes fly on a straight line, form one airport to another airport. For example, when I fly from Lisbon to New York, I expect that the plane always goes towards the West, even if the pilots sometimes deviate a little to avoid a storm on the route.
Obviously, we need a system that automatically controls the amount of deviation of a plane during a flight.
Write a program that, given a flight path, computes the flight angle.
The flight path is the sequence of the flight points of a plane during a flight, each represented by its x-y coordinates.
In a normal flight, the flight angle is represented by a pair of vectors: the counterclockwisemost flight vector and the clockwisemost flight vector.
A flight vector is a vector defined by two consecutive flight points.
We say that a vector u is more counterclockwise than a vector v if changing from the direction of v to the direction of u corresponds to turning to the left; likewise, we say that a vector u is more clockwise than a vector v if changing from the direction of v to the direction of u corresponds to turning to the right.
Note that, given a set of vectors all in the same half-plane, a counterclockwisemost vector u is a vector in the set for which no other vector in the set is more counterclockwise than u, and likewise for the clockwisemost vector.
A normal flight is one where the plane never turns back more than 180 degrees, on any part of the flight path. In other words, a flight is normal if all the flight vectors are in the same half-plane.
The first line of the input contains one integer, N, representing the number of flight points.
N lines follow; each line contains contains two integer numbers, Xi and Yi, for i from 1 to N, separated by one space, representing the x-y coordinates of the i-th flight point.
For a normal flight, your program shall print four space separated integers: the first two represent the earliest counterclockwisemost flight vector; the remaining two represent earliest clockwisemost flight vector.
For the purpose of the above specification, we say that a vector v is earlier than another vector u if the first occurrence of v occurs before the first occurrence of u in the flight path.
If the flight is not normal, your program shall print the coordinates of the last flight points that belongs to the initial normal part of the flight.
| 2 | ≤ N | ≤ 10,000 | Number of points in the flight path |
| −109 | ≤ Xi, Yi | ≤ 109 | Coordinates of points |
The following constraints also apply to all the input test cases:
8 -350 -200 -100 -100 0 -100 100 200 200 200 300 100 300 -100 350 -150
100 300 0 -200
The image below represents the flight path.
The third vector, with components <100, 300>, is the counterclockwisemost; the sixth vector, with components <0, −200>, is the clockwisemost.
10 -150 250 -200 150 -300 50 -200 -50 -100 -50 0 50 100 100 200 100 200 200 300 100
200 100
The image below represents the flight path.
The angle of the eight vector and the second vector is greater than 180 degrees. Actually, this is also true for the angle of the eight vector and the first vector. But note that the angle of the second vector and the fifth vector is exactly 180 degrees.
The normal part of the flight ends at point <200, 100>.
This document was translated from LATEX by HEVEA.