Jasper lives in Grid City. He is quite obsessive and so are we. Everything — no exceptions granted — must be where it should. No street is out of line, no house is out of place, no intersection is misaligned.Jasper lives in Grid City. He is quite obsessive and so are we. Everything — no exceptions granted — must be where it should. No street is out of line, no house is out of place, no intersection is misaligned.
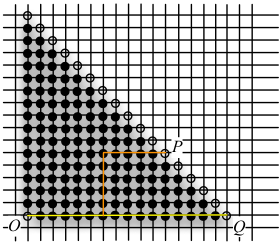
The thing is: Jasper works for the cable company and must ensure that all the intersections (nodes) in the main diagonal get the signal in optimal time, using the smallest amount of cable in the process as digging is expensive.
In the figure, the source of the signal is the white node in the lower left corner, O, whereas the destinations of the signal are the white intersections in the main diagonal. The signal must go through cables along the horizontal and vertical lines (the streets). For example, to reach Q from O along the yellow line, Jasper would spend 16 hops of cable. To route to P, he could then just use the extra 10 hops of cable along the orange path. Overall he needs to ensure that the signal reaches all the 17 destinations in 16 hops, using as little cable as possible.
You should determine the minimal length of cable that is necessary to reach all destinations in the main diagonal in optimal time (i.e., the signal must reach all the white nodes in the main diagonal at the same time).
The number of instances to solve, T, in the first line and the side of the triangles (in terms of hops), N, in each of the following lines.
The minimum length of cable, in hops, necessary to reach all the nodes in the main diagonal in optimal time. One line per triangle in the same order as in the input.
| 1 ≤ T ≤ 1,000 | Number of instances of the problem |
| 1 ≤ N ≤ 10,000,000 | Triangle side |
5 1 2 3 4 80
2 5 8 12 520
This document was translated from LATEX by HEVEA.