Problem G: Risky Maze

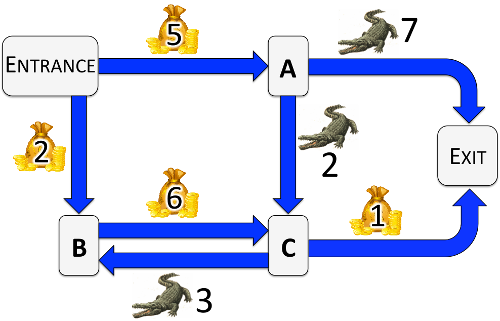
Dirk’s next challenge is a risky game. The game consists in walking through a maze of (one way) corridors, connecting small rooms. Players enter the maze through the Entrance room and leave it from another room, the Exit. At the Entrance, they receive an unlimited credit card with zero balance and have no gold coins.

In each corridor there is:

• either a bag of gold coins;
• or a moat with crocodiles, a (raised) drawbridge and an Automatic Toll Booth.
  In this case, to cross the corridor, the bridge must be lowered, which happens when the player pays the amount of gold coins written on the corridor walls. If the player does not have enough coins, he can use his credit card to pay the rest.

The amount of coins in a bag or required to lower a bridge varies depending on the corridor. Every time a player walks the same corridor, he finds himself in the same situation: either there is always a bag containing the same number of gold coins, or there is always a raised bridge, which is lowered with the same amount of gold coins. No corridor has both a bag and a bridge.

Each corridor has an arrow painted on the floor indicating the direction in which players are allowed to move. Backtracking is strictly prohibited. The game ends as soon as the player arrives at the Exit (which is reachable from any room). At that moment, it is seen if the player is in the money (won gold coins) or still owes money on his credit card.

In spite of his anxiety, Dirk has already decided to enter the game. Since he is fond of the number 3, immediately before entering the maze, he asked the organization if he could lose money even if he arrived at the Exit having passed through at most 3 (not necessarily distinct) corridors.

Could you answer that question? It can be tricky!

• With the maze depicted in the figure, the answer is yes. If Dirk goes from the Entrance to room A (collecting 5 gold coins) and then from room A to the Exit (spending 7 gold coins to lower the drawbridge), he passes through 2 corridors and loses money.
• With a similar maze, where only 5 gold coins were required to lower the bridge from A to the Exit, the answer would be no. There are only three ways to arrive at the Exit crossing at most 3 corridors (Entrance → A → Exit, Entrance → A → C → Exit, and Entrance → B → C → Exit), and in any of them the player does not lose money.
• And if Dirk was fond of the number 1? The answer should be impossible, because he cannot arrive at the Exit passing through only 1 corridor.

Notice that Entrance → B → C → B → C → Exit is a way to arrive at the Exit passing through 5 corridors.

Task

Given the number N Dirk is fond of and a maze description, the goal is to find out the correct answer to Dirk’s question: Can he lose money even if he arrives at the Exit having passed through at most N (not necessarily distinct) corridors?

Input

The first line of the input has three integers: N, R, and C. N is the number Dirk is fond of, R is the number of rooms, and C is the number of corridors. Rooms are identified by integers, ranging from 0 to R−1. The Entrance is room 0 and the Exit is room R−1.

Each of the following C lines contains two different integers, r₁ and r₂, the letter B or the letter C, and an integer G. The first two numbers indicate that there is a corridor from room r₁ to room r₂. If the letter is B, the corridor has a bag with G gold coins. If the letter is C, the corridor has crocodiles and the drawbridge is lowered with G gold coins. It is guaranteed that no corridor starts at the Exit (that is, r₁ ≠ R−1).

Output

The output has a single line with the answer to Dirk’s question. The answer is impossible when Dirk cannot arrive at the Exit passing through at most N (not necessarily distinct) corridors. The answer is yes when Dirk can arrive at the Exit passing through at most N (not necessarily distinct) corridors and there is a way of doing that in which he loses money. The answer is no in all other cases.

Constraints

3 5 7
1 4 C 7
0 1 B 5
0 2 B 2
1 3 C 2
2 3 B 6
3 2 C 3
3 4 B 1

yes

3 5 7
1 4 C 5
0 1 B 5
0 2 B 2
1 3 C 2
2 3 B 6
3 2 C 3
3 4 B 1

no

1 5 7
1 4 C 7
0 1 B 5
0 2 B 2
1 3 C 2
2 3 B 6
3 2 C 3
3 4 B 1

impossible

This document was translated from L^AT_EX by H^EV^EA.